Wie angekündigt ist diese Seite auf das Bildungsportal Niedersachsen umgezogen. In Kürze stellen wir Ihnen an dieser Stelle eine hilfreiche Übersicht über die Angebote des Niedersächsischen Bildungsservers (NiBiS) zur Verfügung.
Lösen von Exponentialgleichungen (im Rahmen des Themas Wachstumsprozesse)
Im Folgenden finden Sie eine Übungseinheit zum Thema "Lösen von Exponentialgleichungen (im Rahmen des Themas Wachstumsprozesse)", die sich direkt an Schülerinnen und Schüler richtet. Geeignet für Klasse 10 (Gymnasium).
Zu den Aufgaben findet man Links mit "Hinweisen" für begleitende Erwachsene, die unten aufgeführt werden.
WORUM geht’s?
Im Unterricht werden Wachstumsprozesse untersucht. Eine wesentliche Rolle spielen dabei sogenannte exponentielle Prozesse. Bei einem exponentiellen Prozess vervielfacht sich eine Größe (z.B. eine Fläche oder eine Anzahl) in gleichen Zeiträumen jeweils mit dem gleichen Faktor (z.B. könnte sich eine Anzahl pro Woche verdoppeln).
Exponentielles Wachstum wird durch einen Funktionsterm der Form f(x) = a ∙ bx beschrieben. Dabei ist a der sogenannte Anfangsbestand und b der Vervielfachungsfaktor pro Zeiteinheit von x.
Sucht man bei exponentiellen Prozessen den Zeitpunkt, zu dem eine bestimmte Größe (z.B. Fläche oder Anzahl) erreicht ist, so muss man Gleichungen der Art
bx = y lösen.
Beispiel: Die Frage nach dem Zeitpunkt, zu dem eine Bakterienpopulation vom Anfangsbestand 20, die sich wöchentlich verdoppelt, den Bestand 10000 erreicht hat, führt auf die Gleichung: 20 ∙2x = 10000.
Das Besondere und zunächst auch die Schwierigkeit liegt bei dieser Art von Gleichungen – den Exponentialgleichungen – darin, dass die gesuchte Größe im Exponenten steht.
Phase 1 – Wiederholung (Hinweis)
Aufträge:
- Wiederhole mit Hilfe deines Schulbuches das Basiswissen zum Logarithmus .
- Bearbeite nach eigener Auswahl einige Grundlagenaufgaben, damit du ....
- ....den Wechsel von der Potenzschreibweise (Exponentialgleichung) in die logarithmische Form sicher durchführst (Beispiel log6 (216) = 3 oder 63 = 216) und
- ....für „einfache Logarithmen“ rationale Zahlen angeben kannst (Beispiel: log2 (16) ist 4, denn 24 = 16).
Tipp: Du kannst dich mit deinem Taschenrechner kontrollieren. - ... erkennst, dass Logarithmieren und Potenzieren sich gegenseitig aufheben, d.h. b logb (x) = x und logb (bx ) = x. (x, b > 0 , b ≠ 1)
- Möchtest du noch mehr und umfangreiches Hintergrundwissen erwerben? Hier ist eine geeignete Quelle, in der auch die Logarithmengesetze aufgeführt werden, die beim Lösen von Exponentialgleichungen angewendet werden können: https://de.wikipedia.org/wiki/Logarithmus (Hinweis)
Phase 2 – Erarbeitung von Strategien
Vorbereitung: Du benötigst für diese Phase
- ... die App „Photomath“ .
- ... deinen grafikfähigen Taschenrechner oder GeoGebra (Hinweis)
- Scanne mit der App Photomath die folgenden Exponentialgleichungen und lasse die Lösungsschritte anzeigen (Hinweise).
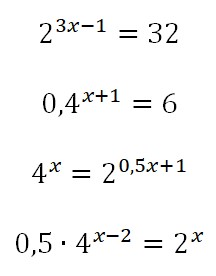
-
Beschreibe und vergleiche die Strategien, die die App in den Lösungsschritten vorschlägt, indem du die Lösungsschritte nachvollziehst und Gemeinsamkeiten und Unterschiede benennst.
Hinweis:
Wenn du das Basiswissen zu Logarithmen gut beherrschst, kannst du bei einfachen Exponentialgleichungen die Lösung direkt angeben.
- Die App bietet neben der rechnerischen Lösung auch eine graphische Darstellung und Lösung an.
Für die dritte Gleichung ergibt sich:
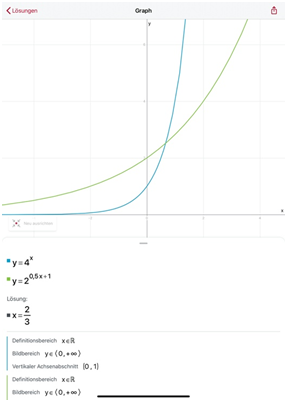
- Erläutere wie sich eine Näherungslösung der Gleichung 4x = 2(0,5x+1) aus dieser Darstellung ergibt (Hinweis).
- Stelle die Graphen zu den Exponentialfunktionen
f(x) = 0,5 ∙ 4x
g(x) = 2x
dar.
Bestimme den Schnittpunkt graphisch (Hinweis).
Gebe eine Bedeutung des Schnittpunktes für einen fiktiven Sachzusammenhang an.
Phase 3 – Anwendung und Übungen
- Berechne jeweils die Lösung der Gleichung. Kontrolliere deine Ergebnisse mit Photomath oder deinem Taschenrechner (z.B. mit dem „solve“-Befehl) (Hinweis).
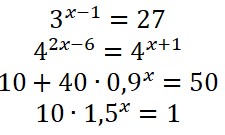
- Gebe zwei Exponentialgleichungen an, die als Lösung x = 2 haben.
-
Eine Bakterienart vermehrt sich so, dass sie jeden Tag ihre Anzahl verfünffacht.
Bestimme mit zwei alternativen Wegen den Zeitpunkt, zu dem aus 100 Bakterien 5000 geworden sind (Hinweis).
-
Die Graphen der Exponentialfunktionen f und g mit f(x) = 5 ∙ 2x und g(x) = 6 ∙ 0,5x haben einen Schnittpunkt (Hinweis).
Skizziere die zugehörigen Graphen und bestimme den Schnittpunkt näherungsweise.
Berechne die Koordinaten des Schnittpunkts.
- In der Abbildung sind die Graphen zu der Exponentialfunktion f und der linearen Funktion g abgebildet (Hinweise).
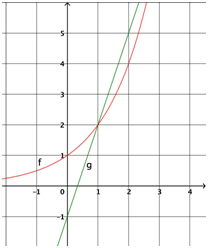
Begründe, dass die Graphen einen weiteren Schnittpunkt haben müssen.
Bestimme die Koordinaten beider Schnittpunkte.
Phase 4 – Reflexion
Auftrag:
Reflektiere deine Kompetenz zum Thema „Exponentialgleichungen“, indem du zwei der folgenden Anregungen ausführst.
- Fasse zusammen, welche grundsätzlichen Möglichkeiten zum Lösen von Exponentialgleichungen du kennst.
- Beschreibe allgemein, in welchen Zusammenhängen Lösungen von Exponentialgleichungen von Interesse sind. Nenne ein konkretes Anwendungsbeispiel.
- Vergleiche deine rechnerischen Strategien zum Berechnen der Lösung einer Exponentialgleichung mit der Berechnung von Lösungen quadratischer Gleichungen
(z.B. 25 = x2 - 8 x + 16 und 0 = x 2 - 8 x + 16) - Entwerfe eine eigene Aufgabe zum Thema Exponentialgleichungen mit einem Anwendungszusammenhang.
- Stelle das Thema in einem kurzen Lernvideo deinen Mitschülerinnen und Mitschülern vor.
- Untersuche, ob es Exponentialgleichungen gibt, die keine Lösung besitzen.
- Stelle ein Mindmap zum Thema „Exponentialgleichungen“ zusammen
- Formuliere (deine) offenen Fragen an das Thema.
Hinweise zu den Aufgabenteilen:
Phase 1 – Wiederholung: In jedem Schulbuch Mathematik Klasse 10 findet sich eine Definition zum Logarithmus. Wesentlich ist der Zusammenhang: logb (y) = x bedeutet dasselbe wie bx = y. Beim Logarithmieren sucht man Exponenten.
(ausgewählte Beispiele: EdM: Seite 110, NW: Seite 157).
Hintergrundwissen: Der Auftrag ist optional für interessierte Schülerinnen und Schüler. Die Logarithmengesetze finden sich auch in den meisten Schulbüchern als optionale Erweiterung.
Datum der Quelle: 6.4.2020
Apps: Die App Photomath ist kostenfrei und kann vielfach als „Tutor“ genutzt werden.
GeoGebra ist eine leistungsstarke Mathematiksoftware, die als App für Tablets und PCs kostenfrei zur Verfügung steht. https://www.geogebra.org
(Für Smartphones stehen ebenso kostenfreie Apps zur Verfügung, die allerdings (zur Zeit) nicht den vollen Funktionsumfang haben.)
Die Gleichung kann aus dem nebenstehen Text gescannt werden oder alternativ separat notiert und gescannt werden. Nach dem Scan (und der Kontrolle der Einlesung) kann über „Lösungsschritte anzeigen“ folgende Darstellung erreicht werden:

Optionale Hilfen zum Beschreiben/Vergleichen der Strategien:
gleiche Basis herstellen, Exponentenvergleich, Potenzgesetze, Logarithmieren der Gleichung mit geeigneter Basis.
Erläuterung des Lösungsansatzes:
Die Gleichung stellt den rechnerischen Ansatz dar, um für zwei Funktionsterme nach den Stellen zu suchen, an denen sie gleiche Werte annehmen. Auf graphischer Ebene ergeben sich Näherungslösungen mit den x-Koordinaten der Schnittpunkte der zugehörigen Graphen der entsprechenden Funktionen zu den Termen.
Hier sollte das Graphikmodul des Taschenrechners oder alternativ GeoGebra genutzt werden.
Darstellen: Im Vergleich zur Lösung der Exponentialgleichung 0,5 ∙ 4x = 2x (die als Lösung x = 1 hat) gehören zu einem Schnittpunkt zwei Koordinatenwerte (hier (1/2)). Die Lösung der Exponentialgleichung liefert dabei die erste Koordinate des Schnittpunktes. Die y-Koordinate ist der Wert an der entsprechenden x-Stelle.
Beide Funktionen könnten ähnliche Wachstumsvorgänge darstellen. Der Schnittpunkt gibt also einen Zeitpunkt an, zu dem beide Prozesse denselben Bestand/dieselbe Anzahl (je nach Zusammenhang) aufweisen.
Berechne: Bei dieser Umkehraufgabe kann eine mögliche Gleichung beispielsweise rückwärts entwickelt werden:
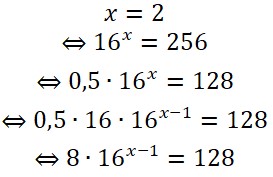
Die Näherungslösung (x ≈ 2,43)
Kann rechnerisch über die Gleichung 100 ∙ 5x = 5000 oder graphisch bestimmt werden.
Die Graphen müssen auch hilfsmittelfrei skizziert werden können.
Als Kontrolle kann der Taschenrechner eingesetzt werden.
Der Punkt hat näherungsweise die Koordinaten S(0,13/5,48).
Ansatz zur Berechnung: 5 ∙ 2x = 6 ∙ 0,5x
(Lösung: x ≈ 0,13 )
Die Aufgabe 5 enthält eine Hürde im Einstieg, da die Funktionsgleichungen nicht gegeben sind. Diese müssen mithilfe der Abbildung aufgestellt werden.
Hinweis: Die Funktionsgleichung zu f hat die Form f(x) = bx, zu g kann die Form g(x) = m ∙ x + c genutzt werden.
Aus der Untersuchung der Wachstumsprozesse ist bekannt, wie sich Bestände, die linear bzw. exponentiell wachsen (langfristig) entwickeln. Daher ist anschaulich bekannt, dass die Steigung des exponentiellen Wachstums stets weiter zunimmt, während die Steigung des linearen konstant ist. Damit muss sich ein weiterer Schnittpunkt ergeben.
Für die Gerade g ergibt sich: g(x) = 3 ∙ x - 1
Für den Graphen zu f ergibt sich: f(x) = 2x
Die Schnittpunkte S(1/2) und Q(3/8) können graphisch oder im rechnerischen Ansatz durch systematisches Probieren bestimmt werden.
Hier ergeben sich individuelle Lösungen, die beispielsweise auch mit Mitschülern abgeglichen oder diskutiert werden könnten.
Bereitgestellt von: Fachberatung Mathematik Sek. I, Niedersächsische Landesschulbehörde, 04.2020



